Why 20 Books?

Among the group of writers I hang around with, the topic of “20 Books” has recently been in the discussion space. Most people I know equate that phrase with the 20 Books to $50K concept made somewhat famous by the gang that ran the conference of the same name (and that eventually moved to the Author Nation group). It’s shorthand lingo that is often misinterpreted as “if you write 20 books, you should be able to make $50K per year.”

That’s wrong, of course, except for when it’s right.

That’s the thing about all writing advice; it’s all wrong except for where it’s right.

There is a reason why 20 books is a pretty good starting place, though. A reason why, especially for an independently published writer, the idea of not getting too caught up in the emotional tides of trying to make a lot of money until you have 20 books makes sense. That reason is discoverability, leverage, and read-through. The more books an author has, the more paths a reader has to both find and make it through their catalog. Assuming the writer is creating books people like to read, the farther those readers will go into said catalog.

I did a free Patreon post yesterday about how Amazon has figured this out, too, and why newer  (or smaller?) writers really ought to change their mindsets around this idea—assuming they haven’t already.

Anyway, lately the question has been coming up “Why 20 Books?”

I’m no marketing scientist, but I am an engineer, and I do understand a few mathematical concepts. The reason is that the more books you have, the more paths a reader has to find, get interested in, and consume your work. And that math is amazing when you plot it.

(Note here: a real mathematician will possibly call me on the fact that I’m simplifying here a little. A real mathematician will tut-tut me for not noting that there are a few ways to frame the question that follows that would make the numbers balloon even farther. I, however, am an engineer. Not a mathematician. I’m happy with my simplification.)

If one asks themself: “Self, if I have written anywhere between one and twenty books, how many different combinations are there of paths people could read through them?” One gets some interesting numbers. This is a pretty fair way of representing discoverability and reader preferences, right? A person could read one book and bounce off. Or could read one series of nine books, and quit me. Or read a one book, and then love everything I do…in a series of different orders.

All of these are different paths.

So, here’s the answer.

Books	Paths
1	1
2	3
3	7
4	15
5	31
6	63
7	127
8	255
9	511
10	1,023
11	2,047
12	4,095
13	8,191
14	16,383
15	32,767
16	65,535
17	131,071
18	262,143
19	524,287
20	1,048,575

Fascinating, right? If you’re a numbers person, this does you fine. But some folks are more visual, so let’s look at it in chart form:

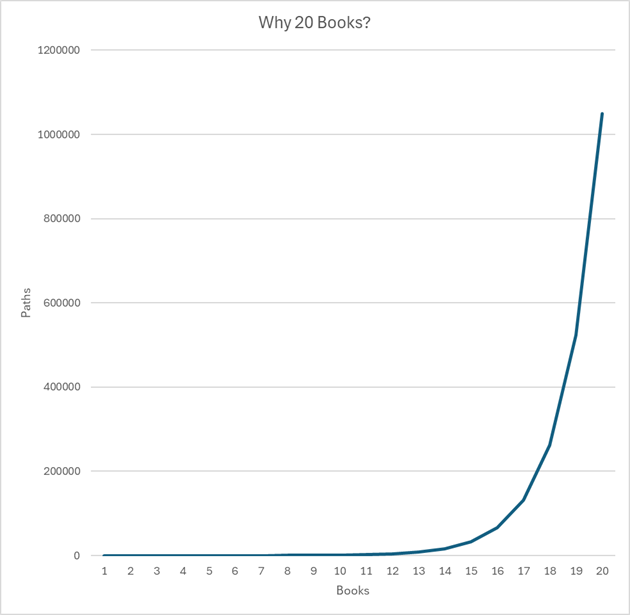
Wow.

Is twenty the right answer?

Maybe it’s fifteen—where the curve is really curving. Or eighteen. Or…well, whatever. Take your number and run with it, but you can see that once you get out to those regions, your discoverability and progression have gone so ballistic that at 20 books there are 1,048,575 different paths a reader can choose to go through your catalog.

Of course, it blows up from there.

At 30 books, the number of paths explodes to 1.07 billion.

Yes, billion, with a “B.”

When you plot that on a non-exponential chart, that makes the curve for twenty books look like a flat line.

So, that’s why twenty books. Turns out that it’s amazingly good fortune that (as Amazon has discovered and has now apparently been pushing for some time) books people actually read don’t spoil.